среда, 5 марта 2014 г.
Вывод
Задача №4
Сказала мама: А сейчас
Про конус будет мой рассказ.
В высокой шапке звездочёт
Считает звёзды круглый год.
КОНУС – шляпа звездочёта.
Вот какой он. Понял? То-то.
Мама у стола стояла,
В бутылки масло разливала.
– Где воронка? Нет воронки.
Поищи. Не стой в сторонке.
– Мама, с места я не тронусь,
Расскажи ещё про конус.
– Воронка и есть в виде конуса лейка.
Ну-ка, найди мне её поскорей-ка.
Воронку я найти не смог,
Но мама сделала кулёк,
Картон вкруг пальца обкрутила
И ловко скрепкой закрепила.
Масло льётся, мама рада,
Конус вышел то, что надо.
Про конус будет мой рассказ.
В высокой шапке звездочёт
Считает звёзды круглый год.
КОНУС – шляпа звездочёта.
Вот какой он. Понял? То-то.
Мама у стола стояла,
В бутылки масло разливала.
– Где воронка? Нет воронки.
Поищи. Не стой в сторонке.
– Мама, с места я не тронусь,
Расскажи ещё про конус.
– Воронка и есть в виде конуса лейка.
Ну-ка, найди мне её поскорей-ка.
Воронку я найти не смог,
Но мама сделала кулёк,
Картон вкруг пальца обкрутила
И ловко скрепкой закрепила.
Масло льётся, мама рада,
Конус вышел то, что надо.
Вычислить объем тела полученный вращением вокруг оси абсцисс.
Задача №2
Теперь, давайте, рассмотрим башню для радиостанции в Москве на Шаболовке, построенной по проекту замечательного русского инженера, почётного академика В. Г. Шухова. Она состоит из частей – гиперболоидов вращения. Причём, каждый из них изготовлен из прямолинейных металлических стержней, соединяющих соседние окружности.(рис.8, 9).
– Рассмотрим задачу.
Найти объем тела, получаемого вращением дуг гиперболы 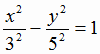 вокруг ее мнимой оси, как показано на рис. 8, где
вокруг ее мнимой оси, как показано на рис. 8, где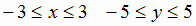
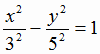 вокруг ее мнимой оси, как показано на рис. 8, где
вокруг ее мнимой оси, как показано на рис. 8, где
Решение.
Задача №1
Рассмотрим отрывок из известной сказки А. С. Пушкина “Сказка о царе Салтане, о сыне его славном и могучем богатыре князе Гвидоне Салтановиче и о прекрасной царевне Лебеде”
И привез гонец хмельной
В тот же день приказ такой:
“Царь велит своим боярам,
Времени не тратя даром,
И царицу и приплод
Тайно бросить в бездну вод”.
Делать нечего: бояре,
Потужив о государе
И царице молодой,
В спальню к ней пришли толпой.
Объявили царску волю –
Ей и сыну злую долю,
Прочитали вслух указ,
И царицу в тот же час
В бочку с сыном посадили,
Засмолили, покатили
И пустили в окиян –
Так велел-де царь Салтан.
Каким же должен быть объем бочки, чтобы в ней поместились царица и её сын?
И привез гонец хмельной
В тот же день приказ такой:
“Царь велит своим боярам,
Времени не тратя даром,
И царицу и приплод
Тайно бросить в бездну вод”.
Потужив о государе
И царице молодой,
В спальню к ней пришли толпой.
Объявили царску волю –
Ей и сыну злую долю,
Прочитали вслух указ,
И царицу в тот же час
В бочку с сыном посадили,
Засмолили, покатили
И пустили в окиян –
Так велел-де царь Салтан.
Каким же должен быть объем бочки, чтобы в ней поместились царица и её сын?
– Рассмотрим следующие задания
1. Найти объем тела, получаемого вращением вокруг оси ординат криволинейной трапеции, ограниченной линиями: x2 + y2 = 64, y = -5, y = 5, x = 0.
Решение.
Ответ : 1163 cm3.
Как вычислить объем тела вращения с помощью определенного интеграла?
Карта- инструктаж "Вычисление объемов"
При помощи определенного интеграла можно вычислить
объем того или иного тела, в частности, тела вращения.
Телом вращения называется
тело, полученное вращением криволинейной трапеции вокруг ее основания.
Подписаться на:
Комментарии (Atom)
.gif)




.gif)
.jpg)







